Big O Notation is a mathematical notation which is used to describe the complexity of an algorithm or a computable function. In computer science, it is used to measure the efficiency of an algorithm, i.e. the amount of time and/or space its implementation uses.
Big O notation is a tool for measuring the complexity of algorithms, often computing the worst case or best case scenarios, which is why it is sometimes refereed to as the “Big Os” (or, Big Order). Big O notation, however, does not measure any particular complexity measure accurately but rather is a tool for approximating complexity.
Big O notation gives a worst-case time complexity measurement and provides a general indication of how well the algorithm can be expected to perform in terms of time and space. By using Big O notation, one can determine the time complexity of a given algorithm, which gives an indication on how the algorithm runs as the input size grows.
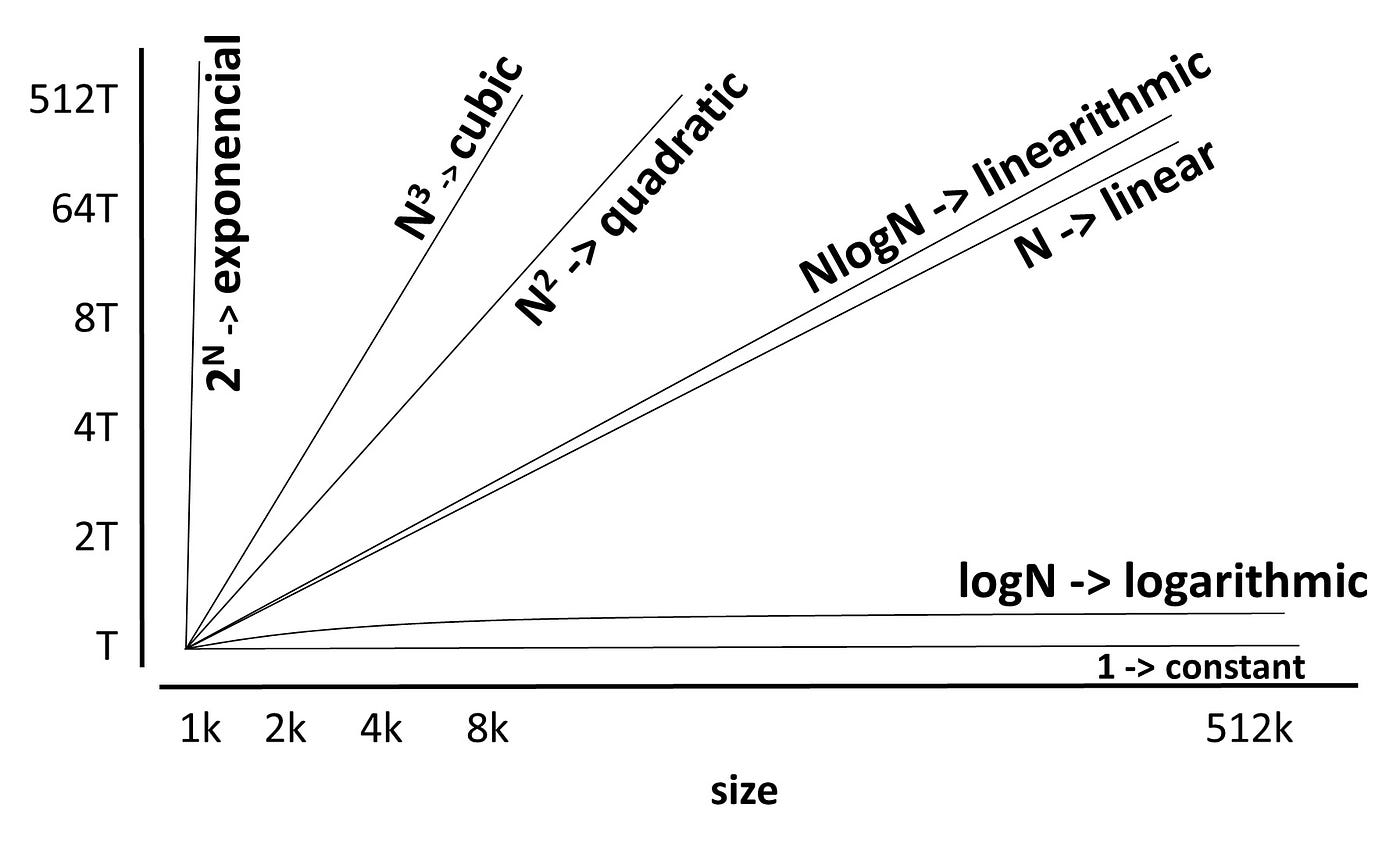
Big O notation is expressed as O(f(n)), where f(n) is the time complexity of an algorithm. Common time complexities that are expressed with Big O notation include O(1) for constant time complexity, O(log n) for logarithmic time complexity, O(n) for linear time complexity, O(n2) for quadratic time complexity, and O(2n) for exponential time complexity.
Big O notation can be used to compare different algorithms, allowing for the identification of the most efficient algorithm for a given problem. By using Big O notation, one can determine the algorithms best suited for solving certain problems while taking resources and time into account.