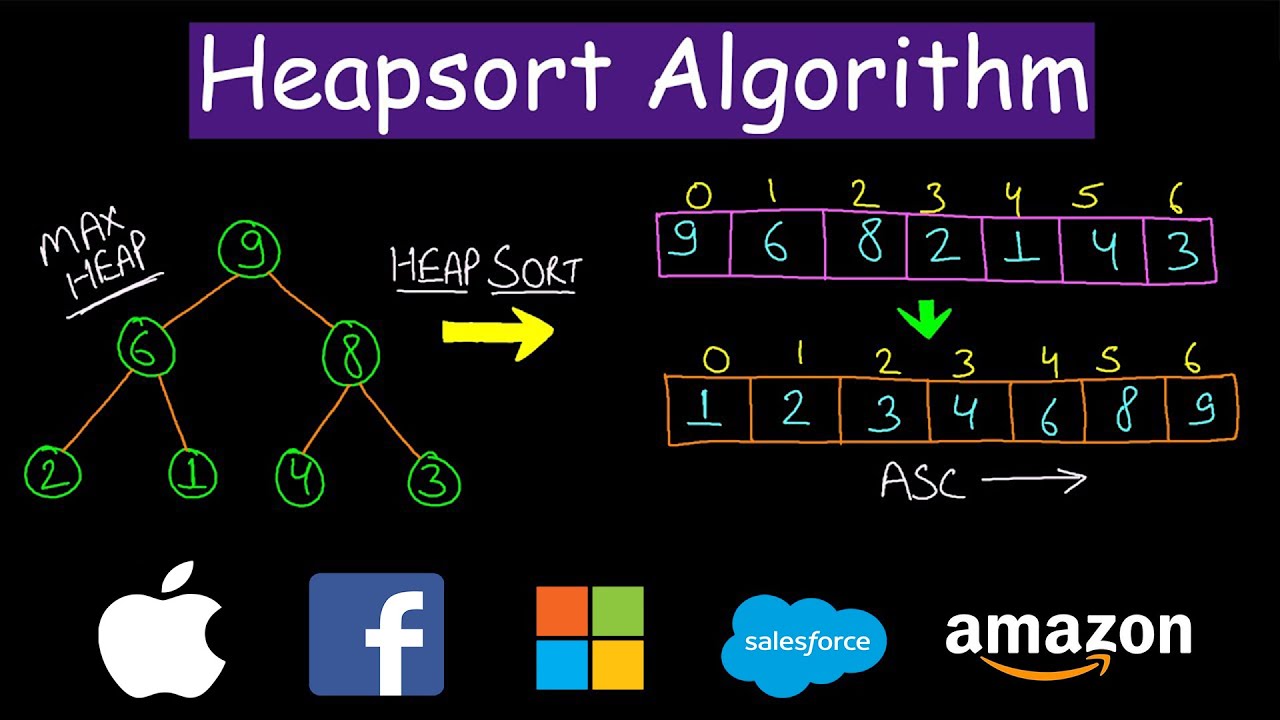
Heapsort is an in-place sorting algorithm used in computer science to produce a sorting algorithm that is more efficient than other sorting algorithms such as Selection Sort, Insertion Sort, and Bubble Sort. The algorithm was developed by J. W. J. Williams in 1964, and is still widely used today.
Heapsort works by first arranging the input data into a Binary Max Heap. A Binary Max Heap is a data structure that satisfies the heap property, where the parent node is always of a greater or equal value than its child nodes. Once this data structure is created, the root node (which has the maximum value in the heap) is swapped with the last element in the data sequence and the size of the heap is decreased by 1. This process is repeated until the heap is completely sorted.
The complexity of Heapsort depends on the type of data structure used to represent the data. If the data structure is of a linear data structure, then the worst-case time complexity of Heapsort is O(nlogn). In the case of a self-balancing binary search tree, the worst-case time complexity of Heapsort is O(n).
Heapsort is an efficient and well-suited algorithm for sorting large amounts of data. Due to its low space complexity, it is also often used in memory-constrained situations. For these reasons, Heapsort is a popular algorithm in many areas of computer science.