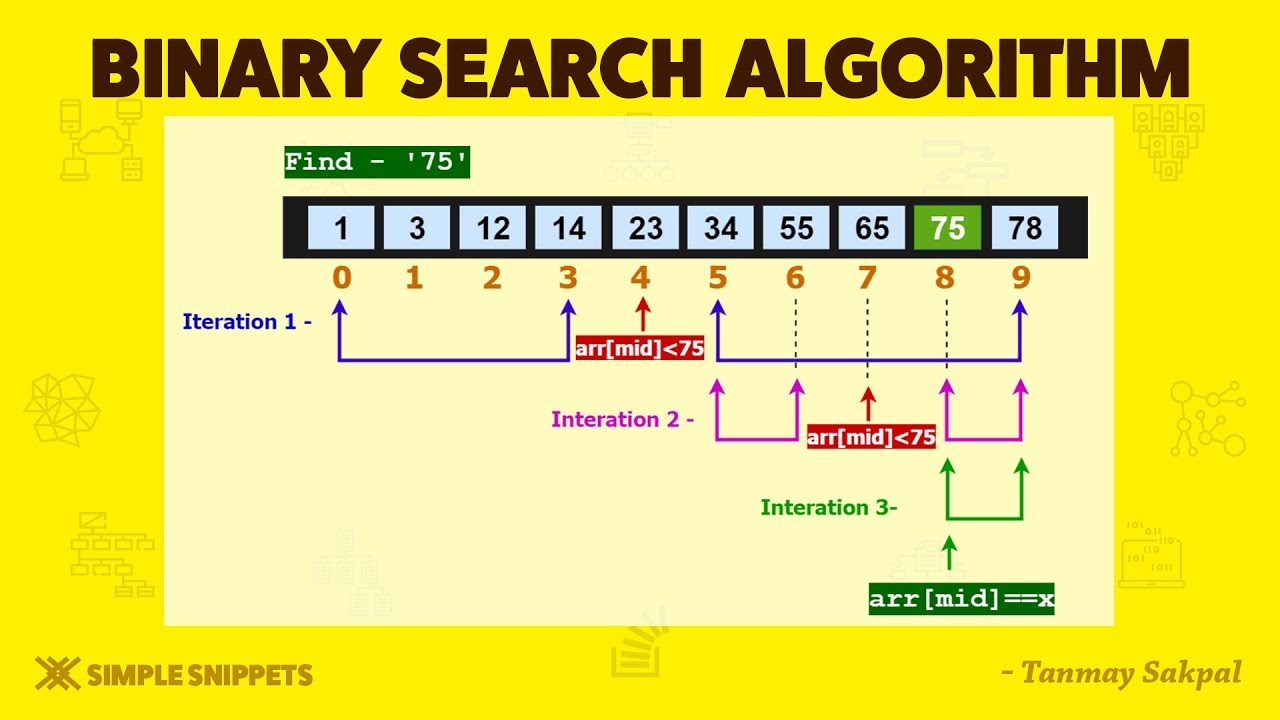
Binary search algorithm is an efficient search algorithm used to locate a specific item in a sorted list within a given time limit. It is also referred to as a half-interval search, logarithmic search, or binary chop. Binary search works by comparing the target value to the middle element of the array. If the little is equal, then the index of the middle element is returned. If the target is less than the middle element, the algorithm continues to search in the lower portion of the array. Similarly, if the target value is greater than the middle element, the algorithm searches in the upper portion of the array. This process continues until the item is located or until the entire array has been searched.
The time complexity of binary search is O(log n), where n is the number of elements in the array. This makes it an efficient algorithm in comparison to linear search, which has a time complexity of O(n). It is important to note that binary search only works on sorted lists, as any discrepancies in the order of elements can result in the algorithm not functioning properly.
Binary search can be used to search through large databases, dictionaries, and arrays. It is also used in compilers and interpreters for syntax analysis and code optimization. Binary search is one of the fundamental algorithms for computer science and is taught in introductory programming classes.