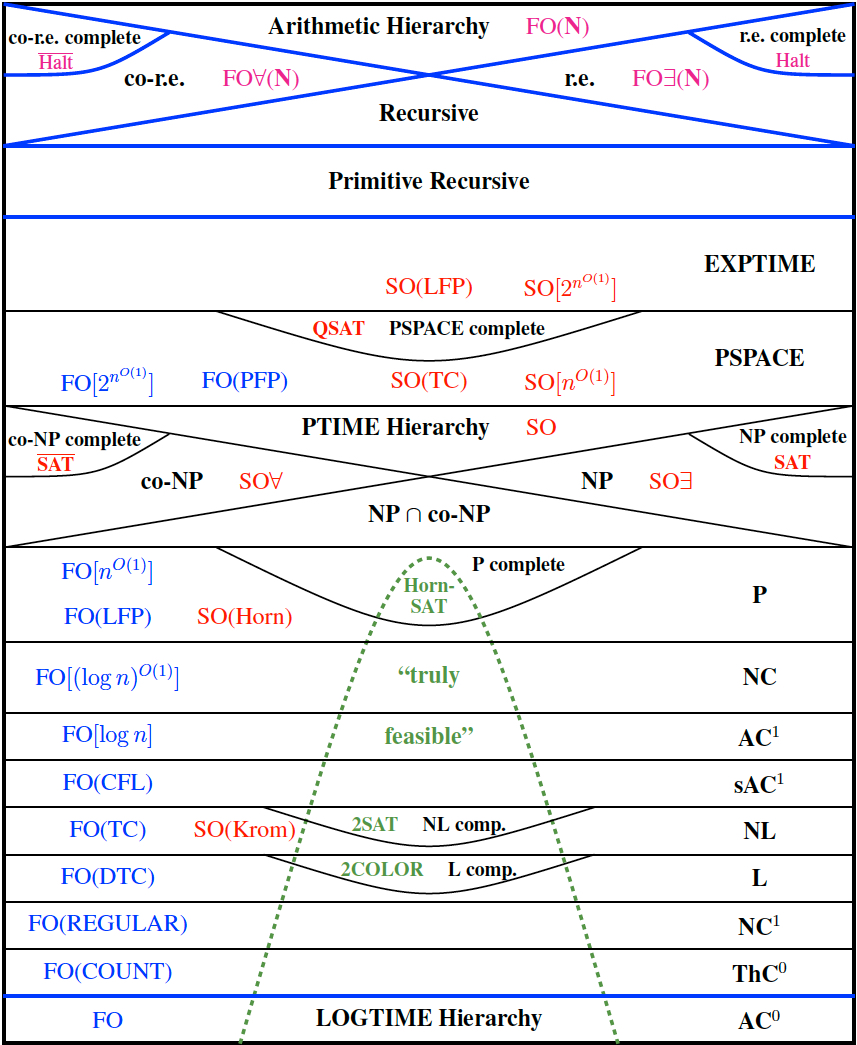
Computability Theory is an area of theoretical computer science and mathematics that studies whether various mathematical problems can be solved using algorithmic processes. It is closely related to the field of recursive function theory. It is also closely associated with the study of computable functions, such as those studied in computability theory and the closely related areas of computable analysis and Turing machines, and its main purpose is to discover the extent to which a given problem is solvable ‘in principle’ by a given computational system, or by any computational system.
Computability theory is concerned with describing the abstract concepts of algorithmic calculations, in particular, the mathematical functions involved in these calculations and the logical operations that govern them. It is also closely related to complexity theory and computer algebra. Computability theory can be seen as a study of the limitations of algorithmic approaches to solving algebraic problems, as opposed to the traditional abstract algebraic approach.
At the heart of computability theory is the question of whether a mathematical function, such as a polynomial equation, can be evaluated in finite time. To answer this question, computability theorists use definitions of computability called the Church-Turing thesis, the Recursion theorem, or the Universal Turing machine. These ideas specify what can and cannot be computed in a given system, and can be used as a basis for proving certain theorems on computability.
Computability theory also provides methods for constructing algorithms that solve certain problems in the most efficient way, such as the Knuth-Bendix algorithm, the Markov Algorithm, and the Rivest-Shamir-Adleman algorithm. These algorithms are commonly used to solve problems in cryptography and linear programming.
In addition to its theoretical applications, computability theory has had a major impact on the development of the modern computer, as well as other areas of engineering and science. It is used in the design of computer systems, as well as in the development of artificial intelligence and machine learning systems. It is also used in mathematicians’ proofs of theorems, and in developing programming languages.