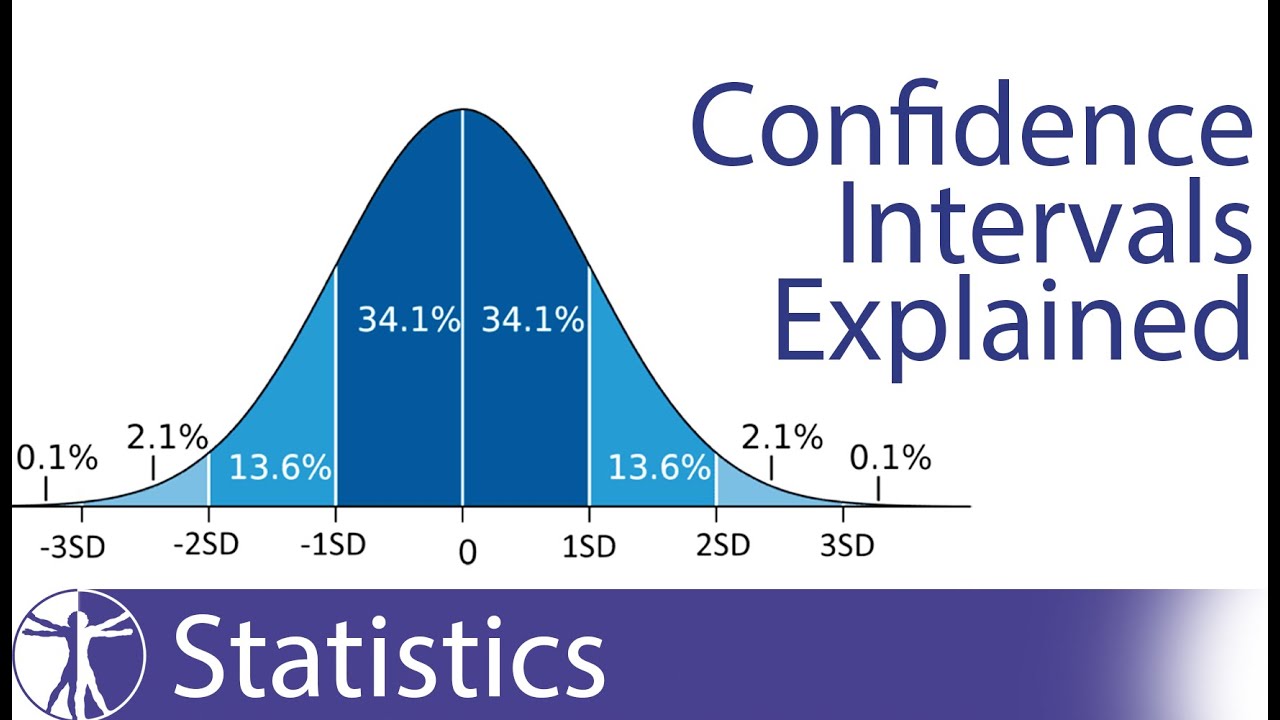
Confidence Interval (CI) is a type of statistical inference used in computer programming. It is used to determine the range in which a population’s true parameter is likely to exist, based on a sample of the population. The CI is typically calculated using the sample mean, sample variance, and sample size.
A CI is used to measure a parameter from a population and provide an interval of reasonable values within which the parameter lies. The CI is a type of hypothesis test, and it is defined by the likelihood that the true parameter will fall within the calculated confidence interval. The confidence interval varies based on the size of the sample. Generally, larger sample sizes lead to a smaller confidence interval as they provide a more accurate estimate of the population’s true parameter.
The formula for a CI can be expressed as: CI = ( X̄ ± z s/sqrt(n) ).
In this formula, X̄ is the sample mean; z is the z-score from the standard normal distribution; s is the sample standard deviation; and n is the sample size.
The confidence obtained from a confidence interval can be expressed as a percentage. This percentage indicates the probability that the true population parameter will be within the calculated CI. The higher the percentage, the more likely it is that the parameter will fall within the CI.
Confidence intervals are used in many areas of computer programming, such as statistics and forecasting. They are used to help detect errors or outliers in a data set, determine the significance of data, or provide a range of expected values for a given data set.