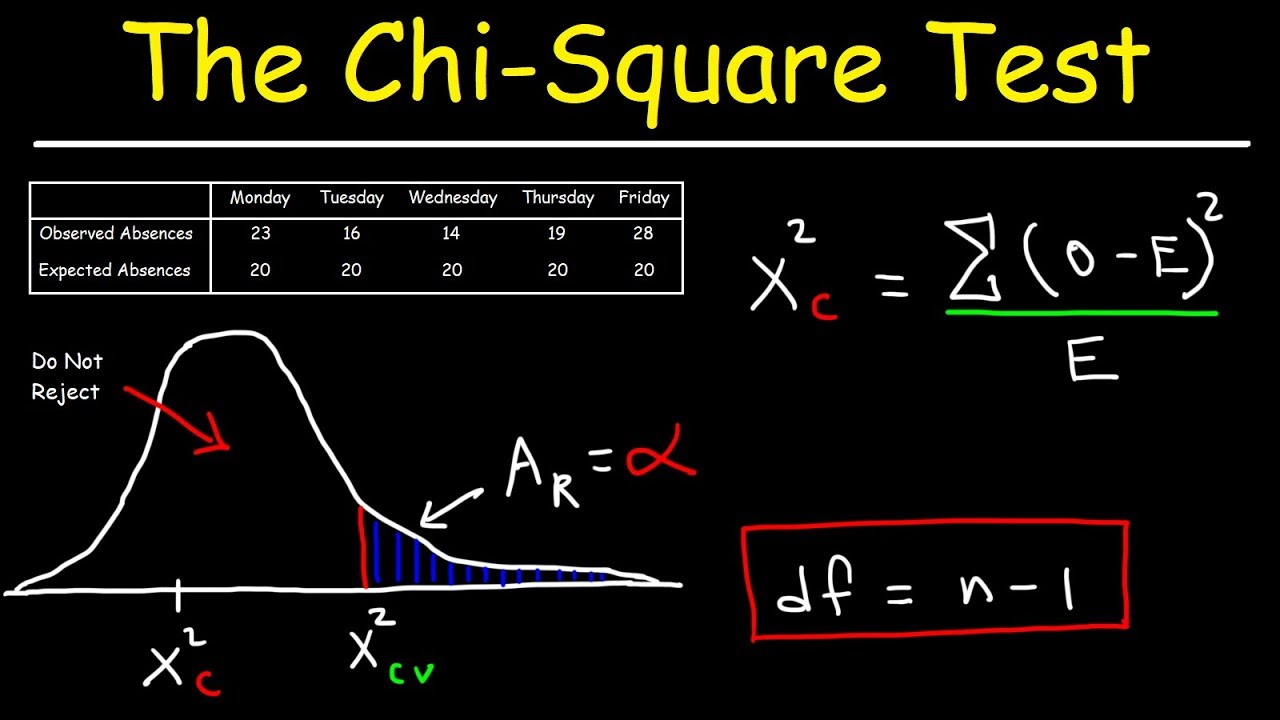
The chi-squared test (χ²) is a statistical method for determining if there is a significant difference between the observed data and the expected data in an relatively small sample. It is commonly used in quality control where there are two possible outcomes, such as healthy and faulty or defective products. The chi-squared test is also used for testing the goodness of fit of an observed data set to a specific theoretical distribution, for comparing observed distribution of frequencies with an expected distribution or for examining the independence of two variables in a contingency table.
The chi-squared test uses the chi-squared statistic to assess the discrepancies between the observed and expected frequencies in one or more categories such as in the case of a die. The chi-squared statistic is calculated as follows: X² = Σ i (o i – e i )²/e i , where o i is the observed frequency, e i is the expected frequency (based on theoretical predictions) and i is a category. The result of the chi-squared test is the probability (p-value) that the difference between the observed and expected frequencies was due to chance. If the p-value is small, then the difference between the observed and expected frequencies is statistically significant; that is, the difference is very unlikely to have occurred by chance.
The chi-squared test can also be used to test the fit of a particular probability model to observed data. It is commonly used to test the hypothesis that two independent variables are related to each other in a two-way contingency table. If the two variables are not related, then the chi-squared test assumes the expected frequencies in each category are equal to the observed frequencies.
The chi-squared test is popular for its simplicity but there are some limitations to its use. The assumptions of the chi-squared test must be carefully considered before calculations are made. For example, if the sample size is too small, the chi-squared test may not be reliable. Furthermore, the chi-squared test assumes that the expected frequencies are greater than five in every category of the contingency table. If this is not the case, then other tests such as Fisher’s exact test must be used.
In conclusion, the chi-squared test is a useful tool for determining if there is a significant difference between the observed and expected frequency of an event. However, caution should be taken when using this test as the assumptions of the test must be carefully considered.